CIELab与CIELch 都可以用来表示物体的颜色,前者简单易懂,因此应用更为普遍。那么,CIELab与CIELch数值一样吗?如何换算呢?本文进行了简单总结。
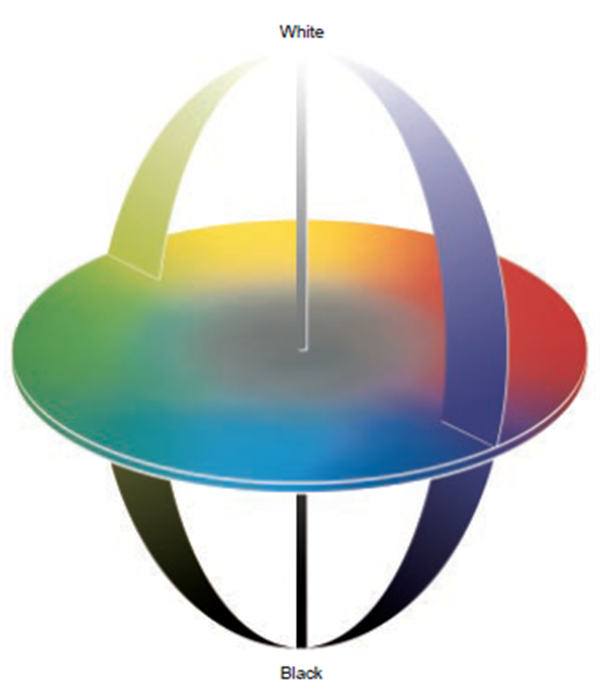
CIELab与CIELch都是基于CIE颜色模型来设定的,这个球状模型中颜色与孟塞尔体系有相似的分布:上下为颜色深浅变化,周向为色相变化,半径为饱和度变化,如上图。
基于此,我们若以三维立体直角坐标体系来定位里边的颜色,则就是我们普遍使用的L*a*b*颜色系统。
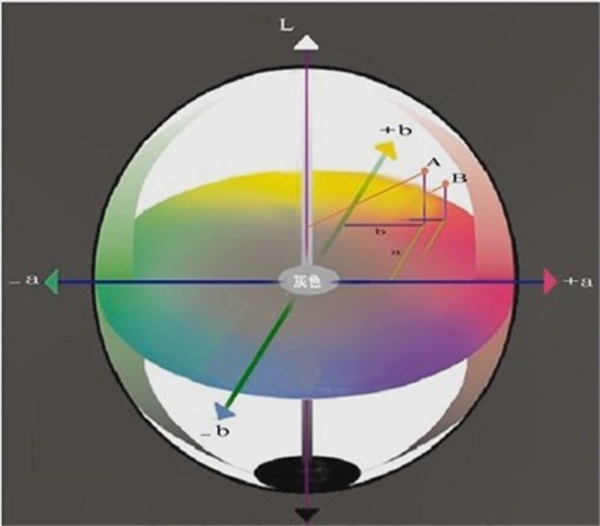
其中L*表示颜色的深浅坐标,a*代表红绿轴坐标,b*代表黄蓝轴坐标,分解成两维如下边示意图。
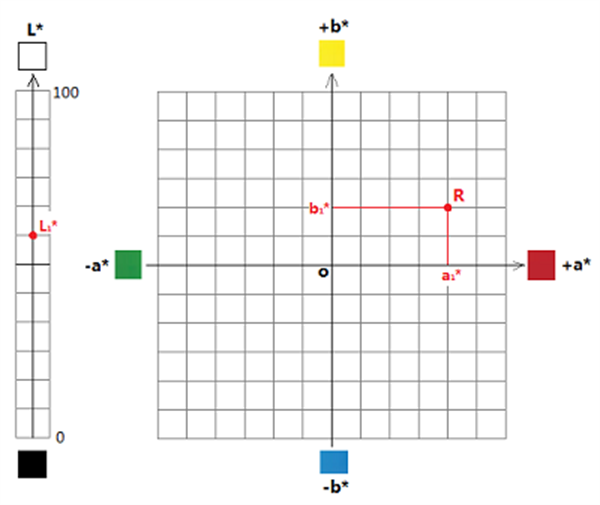
这样空间中任意一点的颜色可以用(L*a*b*)来表示。比如图中的中R点的颜色就可以用(L1*,a1*,b1*)来表示。基于此,两点的色差就可以用坐标差来表示:
ΔL* = L2* - L1*
Δa* = a2* - a1*
Δb* = b2* - b1*
若ΔL*为正数,说明L2* > L1*,L*越大颜色越浅,说明L2*样品偏浅;同理,若ΔL*为负数,说明L2*样品偏深。依次类推:
若ΔL*为正数,则样品偏浅(不够深);
ΔL*为负数,样品偏深(不够浅);
若Δa*为正数,则样品偏红(不够绿);
Δa*为负数,样品偏绿(不够红);
若Δb*为正数,则样品偏黄(不够蓝);
Δb*为负数,样品偏蓝(不够黄);
基于这些信息,配色师可以调整颜色配方,让样品颜色与标准更加接近。
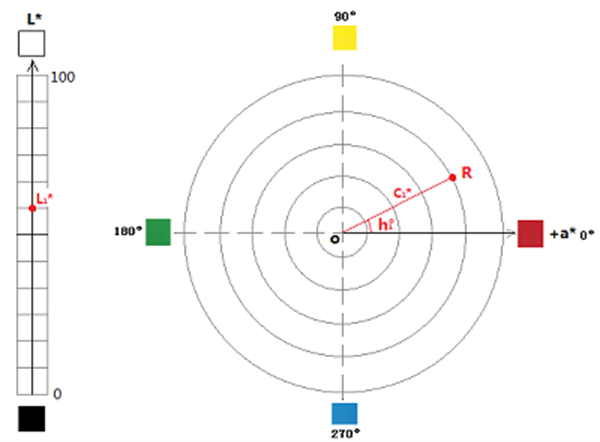
L*C*h°颜色系统也是基于CIE系统,不过它结合了极坐标的方式来定义其中点的位置。
L*依然是深浅坐标,C*代表样品点在a*b*平面投影点到中心的距离(半径),h°代表样品点在a*b*平面投影点与中心连线与 +a* 的夹角。
可见C*是距离,只有正数,正好代表颜色的饱和度(Chroma),越大说明点越靠近边缘,颜色越鲜艳;h°是角度,从0°到360°,正好涵盖了整个色域,h°=90时,正好位于黄色位置,h°=180时,正好位于绿色位置,h°=270时,正好位于蓝色位置。
可见L*C*h°正好对应于颜色的三个属性:明度、饱和度、色调,所以通过这些数据一下即可判断其颜色属性,用来表征颜色更科学。比如前面的R点,用这个系统表征为(L1*,C1*,h1°),如上图:
同理色差计算方法为:
ΔL* = L2* - L1*
ΔC* = C2* - C1*
Δh° = h2°- h1°
同理,若ΔL*为正数,则样品偏浅(不够深);
ΔL*为负数,样品偏深(不够浅);
若ΔC*为正数,则样品偏鲜艳(不够灰暗);
ΔC*为负数,样品灰暗(不够鲜艳);
若Δh°为正数,则样品向逆时针方向偏;
Δh°为负数,样品向顺时针方向偏;
基于这些信息,配色师可以调整颜色配方,让样品颜色与标准更加接近。
需要特别说明的是,Δh°使用的是角度,而其它参数都使用的是长度,那么有时很难通过他们的实际数字来判断哪个变量影响大,所以我们一般通过一个简单的换算将它便成长度度量ΔH*,这样就可以与ΔC*与ΔL*一同比较了。公式如下:
ΔH* = √(ΔL*²+Δa*²+Δb*²-ΔL*²-ΔC*²)
= √(Δa*²+Δb*²-ΔC*²)
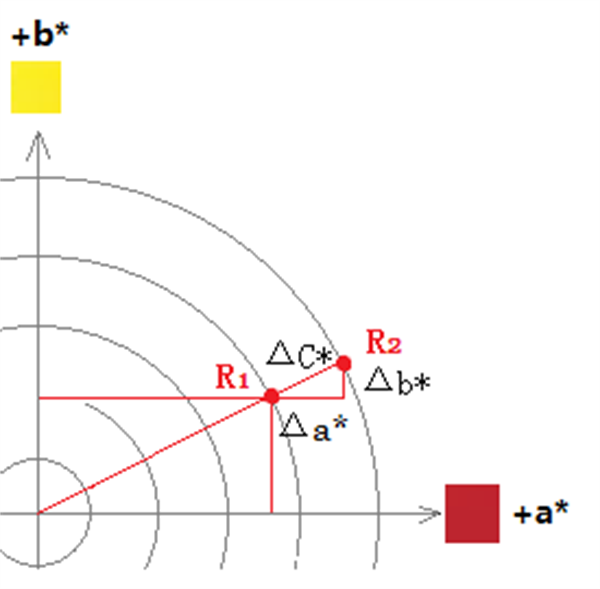
这两个体系坐标的关系如何呢?我们把他们放到一起来,便成上图。
可见L1*相同,而a1*,b1*与C*正好形成直角三角形,h1°是其中的一个角,可见其函数关系为:
C1*² = a1*²+b1*²
tg h1°= b1*/a1*
所以L*a*b*与L*C*h°联系紧密,它们可以相互换算。
那么使用L*C*h°有什么特别优势呢,我们总结如下:
其与颜色三个属性吻合,通过它更容易推断颜色的特性。用L*a*b*时我们要通过a*b*的大小估测样品的色相和饱和度,而通过L*C*h°可以直接获得样品的色调和饱和度信息。
使用ΔL* ΔC* ΔH*更容易对配方进行调整。使用ΔL* Δa* Δb*对配方进行调整时,使用的是红绿黄蓝的偏向信息,有时无法直接进行配方调整,而使用ΔL* ΔC* ΔH*则可以直接获得配方调整方向信息。
我们举个例子:
两个样品的位置分别为R1点和R2点,若以R1为基准点,则R2的偏向为:
Δa*,+ ,偏红
Δb*,+ ,偏黄
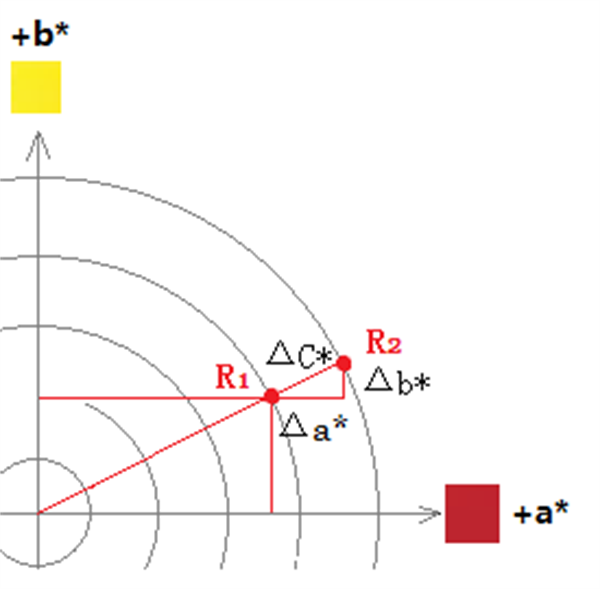
一般样品要么偏红,要么偏黄,这种又偏红又偏黄如何解释呢?那么我们应该是在配方中删减红色颜料含量还是删减黄色颜料呢?这样很容易对配色师造成困惑。
如果用C*H*系统,则结果为:
ΔC*,+ ,偏鲜艳
ΔH*,0 ,无偏差
可以清楚看出色相并无偏差,只是饱和度偏高了。所以彩色颜料相对配比基本无需调整,根据DL*的数据统一减少含量或者添加黑或白颜料即可。
总之L*C*h°三个表征参数与颜色的三个基本属性一一对应,只要理解其含义,无论对于颜色的属性的判断,还是对于颜色偏差的描述,都更加科学,使用更加方便。